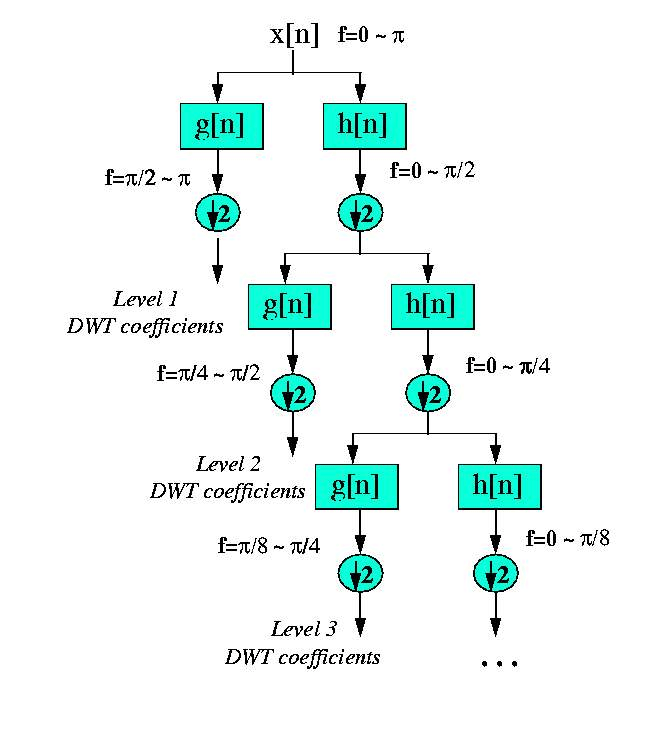
DISCRETE WAVELET TRANSFORM
A
time-scale representation of a digital signal is obtained using digital
filtering techniques. Here, filters of different cutoff frequencies are used to
analyze the signal at different scales. The signal is passed through a series of
high pass filters to analyze the high frequencies, and it is passed through a
series of low pass filters to analyze the low frequencies.
The
resolution of the signal, which is a measure of the amount of detail information
in the signal, is changed by the filtering operations, and the scale is changed
by upsampling and downsampling (subsampling) operations. Subsampling a signal
corresponds to reducing the sampling rate, or removing some of the samples of
the signal. For example, subsampling by two refers to dropping every other
sample of the signal. Subsampling by a factor n reduces the number of samples in
the signal n times.
Upsampling
a signal corresponds to increasing the sampling rate of a signal by adding new
samples to the signal. For example, upsampling by two refers to adding a new
sample, usually a zero or an interpolated value, between every two samples of
the signal. Upsampling a signal by a factor of n increases the number of samples
in the signal by a factor of n.
The
procedure starts with passing this signal (sequence) through a half band digital
lowpass filter with impulse response h[n]. Filtering a signal corresponds to the
mathematical operation of convolution of the signal with the impulse response of
the filter. The convolution operation in discrete time is defined as follows:
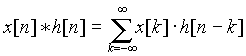
A
half band lowpass filter removes all frequencies that are above half of the
highest frequency in the signal.
The
unit of frequency is of particular importance at this time. In discrete signals,
frequency is expressed in terms of radians. Accordingly, the sampling frequency
of the signal is equal to 2p
radians in terms of radial frequency. Therefore, the highest frequency component
that exists in a signal will be p
radians, if the signal is sampled at Nyquist’s rate (which is twice the
maximum frequency that exists in the signal); that is, the Nyquist’s rate
corresponds to 2p
rad/s in the discrete frequency domain. Therefore using Hz is not appropriate
for discrete signals. However, Hz is used whenever it is needed to clarify a
discussion, since it is very common to think of frequency in terms of Hz. It
should always be remembered that the unit of frequency for discrete time signals
is radians.
After
passing the signal through a half band lowpass filter, half of the samples can
be eliminated according to the Nyquist’s rule, since the signal now has a
highest frequency of p/2
radians instead of p
radians. Simply discarding every other sample will subsample the signal by two,
and the signal will then have half the number of points. The scale of the signal
is now doubled. Note that the lowpass filtering removes the high frequency
information, but leaves the scale unchanged. Only the subsampling process
changes the scale. Resolution, on the other hand, is related to the amount of
information in the signal, and therefore, it is affected by the filtering
operations. Half band lowpass filtering removes half of the frequencies, which
can be interpreted as losing half of the information. Therefore, the resolution
is halved after the filtering operation. Note, however, the subsampling
operation after filtering does not affect the resolution, since removing half of
the spectral components from the signal makes half the number of samples
redundant anyway. Half the samples can be discarded without any loss of
information. In summary, the lowpass filtering halves the resolution, but leaves
the scale unchanged. The signal is then subsampled by 2, since half the number
of samples are redundant. This doubles the scale.
This
procedure can mathematically be expressed as
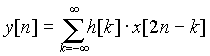……………(7)
Computation
of DWT :
The DWT analyzes the signal at different frequency bands with different
resolutions by decomposing the signal into a coarse approximation and detail
information. DWT employs two sets of functions, called scaling functions and
wavelet functions, which are associated with low pass and highpass filters,
respectively. The decomposition of the signal into different frequency bands is
simply obtained by successive highpass and lowpass filtering of the time domain
signal.
The
original signal x[n] is first passed through a halfband highpass filter g[n] and
a lowpass filter h[n]. After the filtering, half of the samples can be
eliminated according to the Nyquist’s rule, since the signal now has a highest
frequency of p
/2 radians instead of p.
The signal can therefore be subsampled by 2, simply by discarding every other
sample. This constitutes one level of decomposition and can mathematically be
expressed as follows:
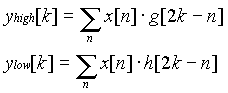…………..(8)
where yhigh[k] and ylow[k] are the outputs of the highpass and lowpass filters, respectively, after subsampling by 2.
This
decomposition halves the time resolution since only half the number of samples
now characterizes the entire signal. However, this operation doubles the
frequency resolution, since the frequency band of the signal now spans only half
the previous frequency band, effectively reducing the uncertainty in the
frequency by half. The above procedure, which is also known as the subband
coding, can be repeated for further decomposition. At every level, the filtering
and subsampling will result in half the number of samples (and hence half the
time resolution) and half the frequency band spanned (and hence double the
frequency resolution).
This
procedure is illustrated below, where x[n] is the original signal to be
decomposed, and h[n] and g[n] are lowpass and highpass filters, respectively.
The bandwidth of the signal at every level is marked on the figure as
"f".
