A filter bank is a structure that decomposes a signal into a collection of sub signals. Depending on the application, these sub signals help emphasize specific aspects of the original signal or may be easier to work when compared to the original signal.
It was Mallat who realized that one can incorporate wavelets into a system that uses cascade of filters to decompose a signal. Each resolution has its own pair of filters: a low pass filter is associate with the scaling function, giving an overall picture of the signal, and high pass filter associated with wavelet, letting through only the high frequencies associated with various details or variations. The two filters complement each other; that which one blocks, the other lets through.
Analysis-Decomposition-From
fine scale to coarser scale
j(t) = å h(n) Ö2 j(2t-n) ------ scaling function
n
When we scale and translate the scaling function will be
j(2jt-k) = å h(n) Ö2 j(2(2jt-n)-n) = å h(n) Ö2 j(2j+1t-2k-n)
n n
= å h(m-2k) Ö2 j(2j+1t-m) where m=2k+n
m
nj = span { 2j/2 j(2jt-k)}
k
f(t) = å cj+1(k)2 (j+1)/2 j(2j+1t-k)
k
is expressible at a scale of j+1 with scaling fn only and no wavelets. At one scale lower resolution, wavelet is necessary for the detail not available at a scale of j.
f(t) = å cj (k)2 j/2 j(2jt-k) + å dj (k)2 j/2 Y(2jt-k)
k k
2 j/2 maintains unity norm of the basis fn at various scales.
cj (k) = å h(m-2k) ò f(t) 2 (j+1)/2 j(2j+1t-k)dt
m
cj (k) = å h(m-2k) cj+1(m) ----------- 1(approximation or scaling coefficient)
m
dj (k) = å h1 (m-2k) cj+1(m) ----------- 2(detail or wavelet coefficient)
m
The filtering of a sequence of numbers (input) is achieved by convolving this sequence with another set of numbers called as the filter coefficients. In other words, to transform a signal into wavelets, at each resolution we convolve the sampled sequence with the sequence of numbers h0 the low pass filter associated with the scaling function and the sequence h1 the high pass filter associated with the wavelet. The h0 and h1 are called the filter coefficients.
If x(n) represents the input sequence and h(n) the filter coefficients, then the output y(n)
N-1
y(n) = å h(k) x(n-k).
k=0
Since there are finite N filter
coefficients then it is called as Finite Impulse Response. If infinite, they are
called Infinite Impulse response. The main design problem is the correct choice
of filter coefficients. Since we are implementing a filter bank for the audio
range, we choose Daubechies 4 as filter coefficients (N=8). ( Please refer to
the previous chapter)
In a multirate filter, two basic operations that take place on the signal are evenly spaced samples of a function of time. They are the downsampler and upsampler. The downsampler takes a signal x(n) as an input and produces an output signal of y(n)=x(2n). In some cases, the down sampling is by a factor greater than two.

In down sampling there is a clear possibility of losing information since half of the data is discarded. The effect in the frequency domain is called aliasing, which states that the result of the loss of information is a mixing of frequency component. If the signal is bandlimited, there is no loss of information caused by downsampling.
Eqn 1 and 2 show that the scaling and wavelet coefficients at different levels can be obtained by convolving the expansion coefficients at scale j by the time reversed coefficients h(n) and h1(-n) then down sampling or deciminating to give the coefficients at next level of j-1. In other words, the scale –j coefficients are filtered by two FIR filters with coefficients h(-n) and h1(-n) after downsampling gives the next coarser scaling and wavelet coefficients. Here h(-n) is low pass filter and h1(-n) is high pass filter.
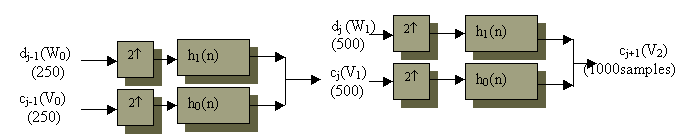
The splitting, filtering and decimation can be repeated on the scaling coefficients to give a filter structure as shown. Repeating this on scaling coefficients is called iterating the filter bank.
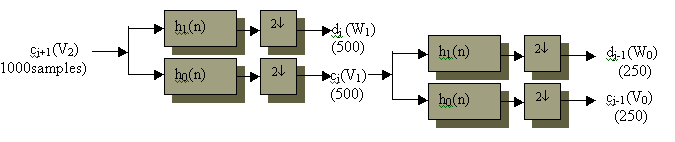
The output of the above filter is as shown below. The first stage of the two banks divides the spectrum (V2) into lowpass and high pass band resulting in scaling coefficients( V1) and wavelet coefficients(W1). The second stage divides that lowpass band(V1) into another lowpass (V0) and high pass band (W0).

The first stage divides the spectrum (1000 samples) into two equal parts (500 each). The second stage divides that lower half into quarters (250 samples each). This results in a logarithmic set of bandwidths. These are called constant-Q filters because the ratio of the band width to the center frequency of the band is constant. Thus, there is no possibility of information that can be lost and a perfect reconstruction can be achieved.
cj+1 (k) = å h(m-2k) cj(m) + å h1(m-2k) dj(m)
m m
For synthesis, we first upsample or stretch the samples and then filter. The upsampling process is done by interpolating zeroes between the original samples.
y(2n) = x(n) and y(2n+1) = 0
Thus the input is stretched to twice its original length by
inserting zeroes. This upsampled signals cj (approximation) and
details dj are convoluted with g(n) and g1(n) which are
low pass and high pass coefficients for reconstruction filter respectively. On
convoluting, we can reconstruct back the original signal. The process of
synthesis is the exact reverse procedure of decomposition.